|
|
| Dipl. -lng. Heinrich Pfeifer |
|
Bandzählwerk in Spielzeit umgerechnet |
|
In FUNKSCHAU 1977, Heft 17, S. 807, war unter dem Titel "Programmierung
von Taschenrechnern" beschrieben, wie sich Rechner-IS quasi
als arithmetikorientierte Mikroprozessoren einsetzen lassen.
Der folgende Beitrag bringt eine typische Anwendung für
solche Schaltungen; ein Taschenrechner-Chip könnte hier
die automatische Umrechnung von einem normalen Bandzählwerk
auf die Tonband-Spieldauer besorgen. Wer sich den Umbau sparen
will, kann natürlich auch "von Hand" rechnen. |
|
Bei der Archivierung von Tonbandaufnahmen ist
auch die Angabe von deren Spieldauer bzw. der noch freien Spieldauer
des Bandes interessant. Aber nur aufwendige Studiomaschinen
besitzen ein Bandzählwerk, das direkt die Spielzeit anzeigt.
Bei Amateurgeräten ist der Zusammenhang zwischen Zählerstand
und Spieldauer nicht linear, da das Zählwerk von einem
Wickelteller angetrieben wird und dieser seine Drehzahl abhängig
vom Wickeldurchmesser ändert. Beispielsweise können
10 Einheiten am Bandanfang einer Spieldauer von einer Minute
entsprechen, am Bandende aber nur noch 20 Sekunden.
Man kann natürlich jede Aufnahme mit der Stoppuhr messen
oder sich auch mit einer Tabelle behelfen, in die man in kurzen
Abständen Zählerstand und Spielzeit einträgt.
Für jeden Bandtyp und jede Spulengröße wäre
eine Tabelle anzulegen; diese Methode ist sehr zeitraubend.
Im folgenden wird eine Formel hergeleitet, die es gestattet,
den Zählwerkstand in die genaue Spielzeit umzurechnen.
Dazu sind vorab für jeden Bandtyp nur zwei Zeitmessungen
vorzunehmen
Theoretische Herleitung
Gesucht ist die Abhängigkeit der Spielzeit t vom Zählwerkstand
z:
t = f(z).
Das Zählwerk zählt die Umdrehungen n eines Wickeltellers,
multipliziert mit einer gerätespezifischen Konstante k:
z = n * k.
Die interessierende Spielzeit t ist über die konstante
Bandgeschwindigkeit v mit der Bandlänge l verknüpft:
t = l/v.
Beides sind lineare Zusammenhänge; es fehlt noch die nichtlineare
Beziehung l = f(n), die aus der Geometrie des Bandwickels
hergeleitet wird.
Das Band wird auf der Spule spiralförmig aufgewickelt.
Der Abstand zweier Spiralwindungen ist konstant gleich der Banddicke
d; dies gilt für den gesamten Wickel. Also handelt es sich
um eine archimedische Spirale; bei dieser ist definitionsgemäß
der Abstand r eines Punktes vom Mittelpunkt proportional dem
Drehwinkel φ, also
r = c * φ
mit c als Proportionalitätskonstante. Daraus folgt, daß
der Abstand zweier Spiralwindungen (φ = 2π) konstant
d = c * 2π beträgt.
Uns interessiert die Länge l des Spiralbogens; hierfür
gilt l = ½ * c * φ², wenn φ wesentlich größer
als 2π ist [1]. Diese Bedingung ist hier grundsätzlich
erfüllt, da uns die Bogenlänge in der Nähe des
Mittelpunktes nicht interessiert. So gilt l = ½ * c *
(2π * n)². Dies ist die Bogenlänge ab Mittelpunkt;
der Bandwickel beginnt jedoch nicht im Spulenmittelpunkt, sondern
beim Spulenkernradius. Diesem Umstand tragen wir Rechnung, indem
wir die hypothetische Bogenlänge l0 = f(n0)
von Mittelpunkt bis Spulenkern subtrahieren:
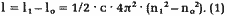
Dabei ist n0 eine Konstante, die vom Kernradius abhängt.
Nehmen wir zunächst an, daß das Bandzählwerk
von der (rechten) Aufwickelspule getrieben wird. Bei leerer
Spule wurde es auf Null gestellt. Der Zählerstand bedeutet
dann z = k * (nt - n0). In Gleichung (1)
können wir nun die Variable n1 durch n1
= z/k + n0 ersetzen; damit ergibt sich:
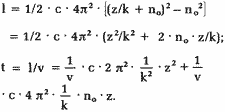
v, c, k und n0 sind Konstanten. Deren Bestimmung
können wir umgehen, indem wir zusammenfassen:

Die Abhängigkeit der Spielzeit t vom Zählerstand z
entspricht also einer quadratischen Gleichung. Dies gilt auch
für Geräte, bei denen das Zählwerk von der (linken)
Abwickelspule getrieben wird; hierbei ergibt sich für a
ein negativer Wert.
Anwendung der Gleichung
Um die Konstanten a und b zu ermitteln, sind zwei Zeitmessungen
erforderlich; die beiden Meßpunkte sollten möglichst
weit auseinanderliegen, etwa in Bandmitte und am Bandende. z1,
t1 seien Zählerstand und zugehörige Spielzeit
etwa in Bandmitte, zmax und tmax am Bandende.
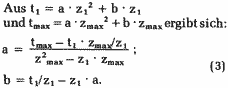
Die beiden Messungen mit anschließender Berechnung von
a und b sind für jeden Bandtyp und jede Spulengröße
einmal vorzunehmen. Da die Stoppuhr während eines Banddurchlaufs
nur zweimal abgelesen werden muß, ist diese Methode weit
bequemer als das Aufnehmen einer ähnlich genauen Tabelle.
Wer das Arbeiten mit einer Tabelle dennoch für angenehmer
hält, kann sich die Tabellenwerte auch mit obiger Formel
errechnen.
Die mit Gleichung (2) errechnete Zeit t ist die Spielzeit vom
Bandanfang bis zum Zählerstand z. Die verbleibende Zeit
vom Zählerstand z bis zum Bandende ergibt sich zu
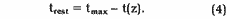
Die Zeit zwischen zwei Zählerständen z1
und z2 beträgt
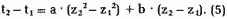
Gelegentlich interessiert auch die Umkehrfunktion von (2); sie
gibt den Zählerstand z an, bei dem eine vorgegebene Spielzeit
t erreicht ist:
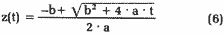
Am besten legt man sich eine Tabelle an, die für jeden
Bandtyp und jede Spulengröße die Werte a, b, tmax
und zmax enthält. Dazu notiert man sich die
Formel (2), eventuell auch (4), (5) und (6). Zur Ermittlung
von a und b aus zwei Messungen dienen die Gleichungen (3).
Die Genauigkeit des Verfahrens wird im wesentlichen durch die
Genauigkeit des Bandzählwerks bestimmt. Ferner ist unbedingt
darauf zu achten, daß beide Spulen den gleichen Kerndurchmesser
haben, damit die Werte a und b auch nach dem Wenden des Bandes
noch gelten.
Zum Aufsuchen einer Stelle auf der zweiten Bandseite muß
üblicherweise zuerst das ganze Band umgespult werden, um
den Zähler auf Null zu stellen. Dies läßt sich
folgendermaßen umgehen: Man legt die volle Spule nach
rechts und die leere nach links und stellt den Zähler nach
dem Aufspulen des Vorspanns auf Null. Dann wird der schnelle
Rücklauf gestartet. Das Zählwerk zählt nun rückwärts,
beginnend mit 9999 (dreistellig: 999). Den abgelesenen Zählerstand
nennen wir zr. Der reelle Zählerstand, der sich
bei Nullstellung am Bandanfang ergeben hätte, beträgt
sodann z = zr + zmax - 10000. (Bei dreistelligem
Zähler ist die Zahl 1000 zu subtrahieren. ) Mit einem Taschenrechner
sind die angegebenen Beziehungen mühelos anzuwenden.
Literatur:
[1] Bronstein, Semendjajew: Taschenbuch der Mathematik. Verlag
Harri Deutsch, Zürich und Frankfurt am Main. |
|
aus: Funkschau 24/1977, Seite
80/81.
Herzlichen Dank an die
Funkschau für die Erlaubnis, diesen Artikel hier zu
veröffentlichen. |
|
|